Answer:

Explanation:
Horizontal Major Axis:
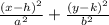
Vertical Major Axis:
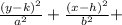
So these two expressions are essentially the same with the only difference being the location of "a" and "b". The length of the major axis will be "2a" and the length of the minor axis will be "2b". The way I remember this is because when you have the horizontal major axis the "a" value is in the denominator of the (x-h) and I think of "x" as a horizontal value, since it moves a point horizontally. When you have a vertical major axis the "a" value is in the denominator of (y-k) and I think of "x" as a vertical value, since it moves a point vertically.
So just by looking at the graph, you can easily determine that the eclipse has a horizontal major axis. This can be further proven, since the distance from the origin on the right side is 28, and the distance from the the top to the origin is only 20.
So you could set up an equation to solve for a, since 2a = length of major axis, but since we're given the two points, the "a" value is really just the length from the origin to the right/left side, and combining these together you get the value of 2a/major axis, but you don't have to do that. So by looking at the graph you'll see the distance from the origin to the right side is 28. This means "a=28"
You can do the same thing here for the "b" value, and since the top is 20 units away from the origin, "b = 20"
So now let's set up the equation:

Square the values in the denominator
