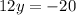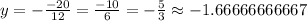Question

Resolver por igualación
2x+3y=2
6x+12y=1

Answer 1

`x = 3.5`

`y\approx1.666666667`

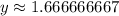
Explanation:

To solve simultaneous equations, at least one of our variables must have the same coefficient. We can easily multiply the first equation by 4 to get 12y on both sides, so let's do that:

`8x + 12y = 8`

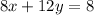
No let's subtract the second equation from the first equation to get the third equation:

`2x = 7`

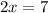
Solve:

`x = 3.5`

Now, we can substitute this value into one of the original equations - let's use the second one:

`21 + 12y = 1`

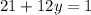
Solve:

`12y = - 20`

`y = - ( - 20)/(12) = ( - 10)/(6) = - (5)/(3) \approx - 1.66666666667`