Question

Factor this:
18x^2+39x-15

Answer 1

Steps for Factoring:

1) Find CM (common factor) for the expression: 3

Factor out 3 =>

`3(6x^(2)+13x-5)`

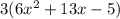
2)Factor the above expression by grouping:

The expression needs to be written as
`6x^(2) + ax+ bx -5`

a and b should add up to 13 and multiply up to -30 (6 × -5)

By Guess & Check we find that the pair is a = -2 and b = 15 (-2+15; -2 × 15)

3) Now we can rewrite
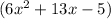`(6x^(2)+13x-5)` as
`(6x^(2) -2x)+(15x-5)\\`

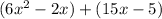
Factor out 2x in the first group and 5 in the second group:

`2x(3x-1)+5(3x-1)\\`

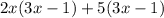
As 3x-1 is on both sides, now we can do the operation: 2x+5 (distributive property)

(3x-1) (2x+5)

The answer is 3(3x-1) (2x+5)

Hope it helps!

Answer 2

answer is:
3(2x+5)*(3x-1)