Question

The equation t^3=a^2 shows the relationship between a planet’s orbital period, T, and the planet’s mean distance from the sun, A, in astronomical units, AU. If the orbital period of planet Y is twice the orbital period of planet X, by what factor is the mean distance increased?

Answer 1

2√2

Explanation:

We can find the relationship of interest by solving the given equation for A, the mean distance.

Solve for A

`T^3=A^2\\\\A=√(T^3)=T√(T)\qquad\text{take the square root}`

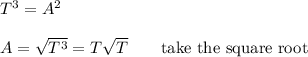
Substitute values

The mean distance of planet X is found in terms of its period to be ...

`D_x=T_x√(T_x)`

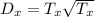
The mean distance of planet Y can be found using the given relation ...

`T_y=2T_x\\\\D_y=T_y√(T_y)=2T_x√(2T_x)=(2√(2))T_x√(T_x)\\\\D_y=2√(2)\cdot D_x`

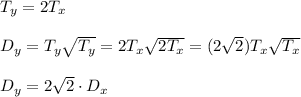
The mean distance of planet Y is increased from that of planet X by the factor ...

2√2