Question

If I have 4.5 liters of gas at a temperature of 33 0C and a pressure of 6.54 atm, what will be the pressure of the gas if I raise the temperature to 94 0C and decrease the volume to 2.3 liters?

Answer 1

15.35 atm

Step-by-step explanation:

Combined Gas Law

`\sf (P_1V_1)/(T_1)=(P_2V_2)/(T_2)`

Temperature must be in kelvins (K).

To convert Celsius to kelvins, add 273.15.

Volume can be in any unit.

Given values:

• P₁ = 6.54 atm
• V₁ = 4.5 L
• T₁ = 33 °C = 33 + 273.15 = 306.15 K
• P₂ =
• V₂ = 2.3 L
• T₂ = 94 °C = 94 + 273.15 = 367.15 K

Rearrange the equation to isolate P₂:

`\sf \implies P_2=(P_1V_1T_2)/(V_2T_1)`

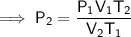
Substitute the given values into the equation:

`\sf \implies P_2=(6.54 \cdot 4.5 \cdot 367.15)/(2.3 \cdot 306.15)`

`\sf \implies P_2=15.34516967`

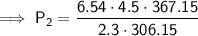
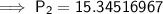
Therefore, the pressure of the gas will be 15.35 atm (2 d.p.).

Answer 2

This is an exercise in the general or combined gas law.

To start solving this exercise, we must obtain the following data:

Data:

• V₁ = 4.5 l
• T₁ = 33 °C + 273 = 306 k
• P₁ = 6.54 atm
• T₂ = 94 °C + 273 = 367 k
• V₂ = 2.3 l
• P₂ = ¿?

We use the following formula:

• P₁V₁T₂ = P₂V₂T₁ ⇒ General Formula

Where

• P₁ = Initial pressure
• V₁ = Initial volume
• T₂ = Initial temperature
• P₂ = Final pressure
• V₂ = Final volume
• T₁ = Initial temperature

We clear the general formula for the final pressure.

`\large\displaystyle\text{$\begin{gathered}\sf P_(2)=(P_(1)V_(1)T_(2) )/(V_(2)T_(1)) \ \to \ Clear \ formula \end{gathered}$}`

We solve by substituting our data in the formula:

`\large\displaystyle\text{$\begin{gathered}\sf P_(2)=\frac{(6.54 \ atm)(4.5 \\ot{l})(367 \\ot{K}) }{(2.3 \\ot{l})(306 \\ot{k})} \end{gathered}$}`

`\large\displaystyle\text{$\begin{gathered}\sf P_(2)=(10800.81)/( 703.8 ) \ atm \end{gathered}$}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf P_(2)=15.346 \ atm \end{gathered}$} }`

If I raise the temperature to 94°C and decrease the volume to 2.3 liters, the pressure of the gas will be 15,346 atm.