Question

A college graduate expects to earn a salary of $55,000 during the first year after graduation and receive a 3% raise every year after that. What is the total income he will have received after ten years?

Answer 1

Answer: $630,513.36

Explanation:

Making a Formula for His Salary on a Given Year

Let's make a table of values to see how much he earns every year after graduation.

1 year -> $55,000

2 years -> 55,000 * 103% = $56,650

3 years -> 56,650 * 103% = 55000 * 103% * 103% = $58,349.50

4 years -> 58349.50 * 103% = 55,000 * 103% * 103% * 103% = 55000(1.03)³

Here, we see that every year, he gets 103% of what he got the previous year, which is also 1.03 times his previous salary.

We also see that we multiply 55000 by 1.03 three times in the fourth year, and two times in the third year. This means that we multiply 55000 by 1.03 n-1 times.

Using this, let's generalize this for n.

n years ->
`55000(1.03)^(n-1)`

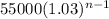
Finding the Sum after Ten Years

We are trying to find his total income after ten years, or the sum of his salary from year 1 to year 10. We can represent this in sigma notation like this

`% Adjusted limits of summation$\displaystyle\sum_(n=1) ^(10) 55000(1.03)^(n-1)$`

This essentially translates to the sum of the first ten terms in the sequence
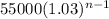`55000(1.03)^(n-1)`, starting at n=1.

Since this is a geometric sequence, or a sequence where we need to multiply by the same number to get to the next term, we can find the sum using the sum of geometric series formula. This formula is as follows:

`S_n=a_1(1-r^n)/(1-r)`

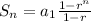
where
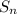`S_n` is the sum of the first n terms,
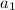`a_1` is the first term, r is the common ratio, and n is the number of terms. In this question,
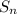`S_n` is the total income after n years,
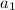`a_1` is his salary after the first year, r is how much his salary increases by each year, and n is the number of years we are calculating the sum for.

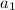`a_1` -> 55000

r -> 1.03

n -> 10

Now that we have the values for each variable, let's plug them in and solve

`S_(10)=55000((1-1.03^(10))/(1-1.03))\\S_(10)=630513.36`

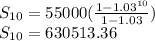
The total income he will have received after ten years is $630,513.36.

Answer 2

$73915.40

Explanation:

→ Find the multiplier

( 3 + 100 ) ÷ 100 = 1.03

→ Multiply by principal amount and raise it to the power of years

55000 × 1.03¹⁰ = 73915.40