Answer:
Speed of fish in still water = 10 m/s
Speed of current = 4 m/s
Explanation:
Let the speed of the fish in still water = x m\s
Let the speed of the current = y m/s
Speed of the fish with the current = x + y
x +y = 14 m/s ------------------(I)
Speed of the fish against current = x -y
x - y = 6 m/s ----(II) &
Add the equations (I) & (II) and 'y' will be eliminated and we can find the value of 'x'.
x + y = 14
x - y = 6 {Now, add)
2x = 20
x = 20/2
x = 10
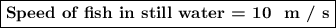
Plugin x = 10 in equation (I)
10 + y = 14
y = 14 - 10
y = 4
