When
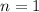 ,
,
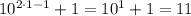
which is of course divisible by 11.
Assume this holds for
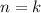 , that
, that
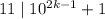
In other words,
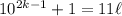
for some integer
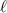 .
.
Use this to show the claim is true for
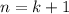 .
.
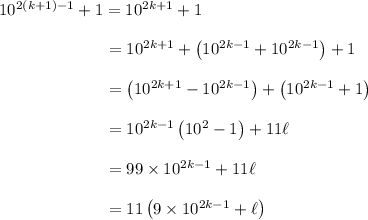
which is indeed divisible by 11. QED
On the off-chance you meant
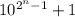 , notice that
, notice that
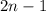 is odd for any integer
is odd for any integer
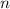 . Similarly
. Similarly
 is odd for all
is odd for all
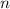 , so the above proof actually proves this automatically.
, so the above proof actually proves this automatically.