- The distance between two points
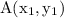 and
and
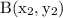 is given by the formula,
is given by the formula,
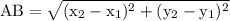
Proof:
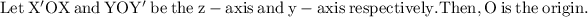
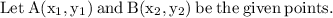
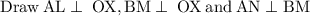
Now,
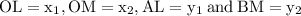
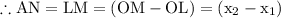
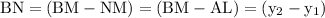
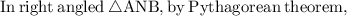
We have,
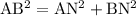
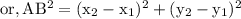
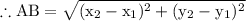
The Given question,
Find the distance of AG if A (4,4) and G (-1,-1).
Solution,
The given points are A(4,4) and G(-1,-1).
Then,
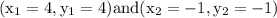
We know that,
The distance formula,
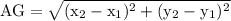
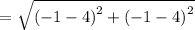
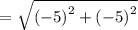
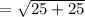
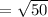
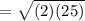
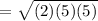
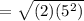
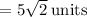
Answered by: