Question

asked Jul 21, 2023 227k views

2 Answers

Lulas · Answer 1 · 2023-07-23T23:29:12+0000

Directrix

Focus

Focus lies in Q3 and above y=1

Then

Perpendicular distance

Find a for the equation

Now the equation is

$\\ \rm\dashrightarrow 4a(y-k)=(x-h)^2$

$\\ \rm\dashrightarrow 4(2)(y-5)=(x+4)^2$

$\\ \rm\dashrightarrow 8(y-5)=x^2+8x+16$

$\\ \rm\dashrightarrow 8y-40=x^2+8x+16$

$\\ \rm\dashrightarrow 8y=x^2+8x+16+40$

$\\ \rm\dashrightarrow 8y=x^2+8x+56$

$\\ \rm\dashrightarrow y=(x^2)/(8)+x+7$

Mariah · Answer 2 · 2023-07-26T19:16:46+0000

${\qquad\qquad\huge\underline{{\sf Answer}}}$

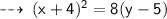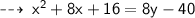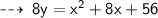
Let's solve ~

Equation of directrix is : y = 1, so we can say that it's a parabola of form : -

$\qquad \sf  \dashrightarrow \: (x - h) {}^(2) = 4a(y - k)$

a = half the perpendicular distance between directrix and focus = 1/2(5 - 1) = 1/2(4) = 2

and since the focus is above the directrix, it's a parabola with upward opening.

$\qquad \sf  \dashrightarrow \: (x - ( - 4)) {}^(2) = 4(2)(y - 5)$

$\qquad \sf  \dashrightarrow \: (x + 4) {}^(2) = 8(y - 5)$

$\qquad \sf  \dashrightarrow \: {x}^(2) + 8x + 16 = 8y - 40$

$\qquad \sf  \dashrightarrow \: 8y = {x}^(2) + 8x + 56$

$\qquad \sf  \dashrightarrow \: y = \cfrac{1}{8} {x}^(2) + x + 7$

Please log in or register to add a comment.