Answer:
a ≈ 16.5 cm , b ≈ 23.8 cm
Explanation:
using the Law of Sines in Δ ABC
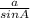 =
=
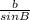 =
=

we require to calculate ∠ C
∠ C = 180° - (42 + 75)° = 180° - 117° = 63°
Then to find a
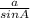 =
=
 ( substitute values )
( substitute values )
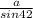 =
=
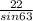 ( cross- multiply )
( cross- multiply )
a × sin63° = 22 × sin42° ( divide both sides by sin63° )
a =
 ≈ 16.5 cm ( to the nearest tenth )
≈ 16.5 cm ( to the nearest tenth )
similarly to find b
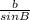 =
=
 ( substitute values )
( substitute values )
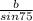 =
=
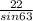 ( cross- multiply )
( cross- multiply )
b × sin63° = 22 × sin75° ( divide both sides by sin63° )
b =
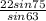 ≈ 23.8 cm ( to the nearest tenth )
≈ 23.8 cm ( to the nearest tenth )