Question

Find the gradient of the tangent to the curve y = (√x + 3)(3√x - 5) at the point where x = 1​

Answer 1

Gradient (slope) is 5.

Explanation:

To find the gradient (slope) of a curve graph at x = x₁ can be done by steps following:

1. Differentiate the function - this is to find a gradient (slope) at any points (technically function of slope)
2. Substitute x = x₁ in the derived function - you'll receive a slope at x = x₁ point.

First, derive the given function which is:

`\displaystyle{y = (√(x)+3)(3√(x)-5)`

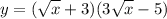
Differentiation can be done two ways - go ahead and expand the expression then derive it or you can use the product rule where it states that
`\displaystyle{y'=u'v+uv'}`

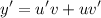
I'll be using product rule:

`\displaystyle{y' = (√(x)+3)'(3√(x)-5)+(√(x)+3)(3√(x)-5)'}`

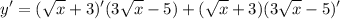
Note that the following process will require you to have knowledge of Power Rules:

`\displaystyle{y = ax^n \to y' = nax^(n-1)}`

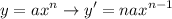
Hence:

`\displaystyle{y'=(1)/(2√(x))(3√(x)-5) + (√(x)+3)(3)/(2√(x))`

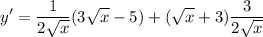
Now we know the derivative. Next, we find the slope at x = 1 which you substitute x = 1 in derived function:

`\displaystyle{y'(1)=(1)/(2√(1))(3√(1)-5) + (√(1)+3)(3)/(2√(1))}\\\\\displaystyle{y'(1)=(1)/(2)(3-5) + (1+3)(3)/(2)}\\\\\displaystyle{y'(1)=(1)/(2)(-2) + (4)(3)/(2)}\\\\\displaystyle{y'(1)=-1 + 2(3)}\\\\\displaystyle{y'(1)=-1 + 6}\\\\\displaystyle{y'(1)=5}`

Finally, we have found the slope or gradient at x = 1 which is 5.

Please let me know if you have any questions!