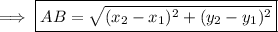Answer:
The distance between two points
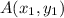 and
and
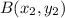 is given by the formula,
is given by the formula,
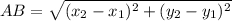
Proof: Let X'OX and YOY' be the x-axis and y-axis respectively. Then, O is the origin.
Let
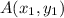 and
and
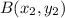
be the given points.
Draw AL perpendicular to OX, BM perpendicular to OX and AN perpendicular to BM
Now,
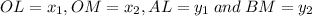
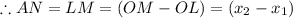
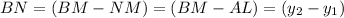
In right angled triangle
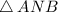 ,by Pythagorean theorem,
,by Pythagorean theorem,
We have,
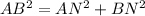
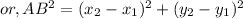
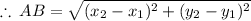
Thus ,the distance between the points A(x_1,y_1) and B(x_2,y_2) is given by,