Question

100 POINTS!!! PLEASE HELP ASAP EXPERTS! PLEASE I'M BEGGING!!

The function H(t) = −16t2 + 64t + 12 shows the height H(t), in feet, of a baseball after t seconds. A second baseball moves in the air along a path represented by g(t) = 10 + 10.4t, where g(t) is the height, in feet, of the object from the ground at time t seconds.

Part A: Create a table using integers 1 through 4 for the 2 functions. Between what 2 seconds is the solution to H(t) = g(t) located? How do you know? (6 points)

Part B: Explain what the solution from Part A means in the context of the problem. (4 points)

Answer 1

A)

`\begin{array}c\cline{1-3} t & H(t) & g(t)\\\cline{1-3} 1 & 60 & 20.4\\\cline{1-3} 2 & 76 & 30.8\\\cline{1-3} 3 & 60 & 41.2\\\cline{1-3} 4 & 12 & 51.6\\\cline{1-3} \end{array}`

Between 3 and 4 seconds.

B) The baseballs will collide between 3 and 4 seconds.

Explanation:

Given functions:

`H(t)=-16t^2+64t+12`

`g(t)=10+10.4t`

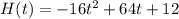
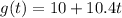
Part A

Substitute the values of t = 1, 2, 3 and 4 into the two functions:

`H(1)=-16(1)^2+64(1)+12=60`

`H(2)=-16(2)^2+64(2)+12=76`

`H(3)=-16(3)^2+64(3)+12=60`

`H(4)=-16(4)^2+64(4)+12=12`

`g(1)=10+10.4(1)=20.4`

`g(2)=10+10.4(2)=30.8`

`g(3)=10+10.4(3)=41.2`

`g(4)=10+10.4(4)=51.6`

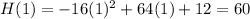
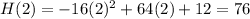
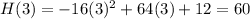
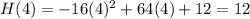
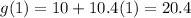
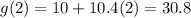
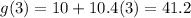
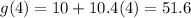
Create a table with the found values:

`\begin{array}c\cline{1-3} t & H(t) & g(t)\\\cline{1-3} 1 & 60 & 20.4\\\cline{1-3} 2 & 76 & 30.8\\\cline{1-3} 3 & 60 & 41.2\\\cline{1-3} 4 & 12 & 51.6\\\cline{1-3} \end{array}`

The solution to H(t) = g(t) is between 3 and 4 seconds as:

When t = 3, H(t) > g(t)

When t = 4, H(t) < g(t)

To prove this, equate the equations and solve for t:

`\implies -16t^2+64t+12=10+10.4t`

`\implies -16t^2+53.6t+2=0`

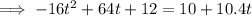
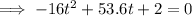
Using the Quadratic Formula to solve for t:

`x=(-b \pm √(b^2-4ac) )/(2a)\quad\textsf{when }\:ax^2+bx+c=0`

`\implies t=(-53.6 \pm √(53.6^2-4(-16)(2)) )/(2(-16))`

`\implies t=(53.6 \pm √(3000.96))/(32)`

`\implies t=3.39, -0.04\:\:(\sf 2\:d.p.)`

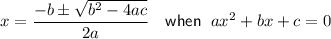
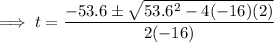
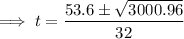
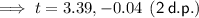
As time is positive, t = 3.39 s (which is between 3 and 4 seconds).

Part B

When the two baseballs are at the same height they will collide.

Therefore, the baseballs will collide between 3 and 4 seconds (when t = 3.39 s).