Answer:
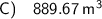
Explanation:
The given composite solid is made up of a cylinder and a cone.
To find the volume of the composite solid, find the volume of the cylinder and the volume of the cone, then add them together.
Volume of a cylinder:
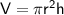
(where r is the radius and h is the height)
Given:
Substitute the given values into the formula and solve for V:

Volume of a cone:
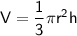
(where r is the radius and h is the height)
Given:
Substitute the given values into the formula and solve for V:

Therefore, the volume of the composite solid is:
