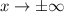Part A

Part B

So, the x-intercepts are
 and
and
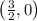
Part C
As
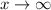 ,
,
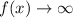 because the leading coefficient is positive.
because the leading coefficient is positive.
As
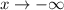 ,
,
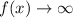 because the degree is even and the leading coefficient is positive.
because the degree is even and the leading coefficient is positive.
Part D
Plot the x-intercepts on the graph, and then find the value of
 at
at
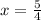 (the midpoint of the two roots) to plot the vertex. Then, draw a curve through these three points that approaches infinity as
(the midpoint of the two roots) to plot the vertex. Then, draw a curve through these three points that approaches infinity as