Question

A 0.80-kg mass attached to the end of a string swings in a vertical circle (radius = 2.0 m). When the mass is at the highest point of the circle, the speed of the mass is 9.0 m/s. What is the magnitude of the force of the string on the mass at this position?

Answer 1

Approximately
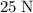`25\; {\rm N}` assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`.

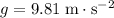Step-by-step explanation:

This mass is in a circular motion of radius
`r`. Hence, when the velocity of the mass is
`v`, the acceleration of this mass should be
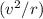`(v^(2) / r)`. The net force on this mass should be
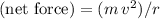`(\text{net force}) = (m\, v^(2)) / r` towards the center of the circle.

When this
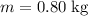`m = 0.80\; {\rm kg}` mass is at the top of this circle, both gravitational pull and the force of the string (tension) point downwards. Hence, the net force on this mass would be:

`(\text{net force}) = (\text{weight}) + (\text{tension})`.

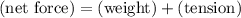Thus:

`\begin{aligned} (\text{tension}) &= (\text{net force}) -(\text{weight})\\ &= (m\, v^(2))/(r) - m\, g \\ &= m\, \left((v^(2))/(r) - g\right) \\ &= 0.80\; {\rm kg}* \left(\frac{(9.0\; {\rm m\cdot s^(-1)})^(2)}{2.0\; {\rm m}} - 9.81\; {\rm m\cdot s^(-2)}\right) \\ &\approx 25\; {\rm kg \cdot m\cdot s^(-2)} \\ &= 25\; {\rm N}\end{aligned}`.