Answer:

Explanation:
Step 3:
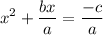 --------------------(1)
--------------------(1)
The next step will be:
- to find the b² for the expression on the left.
How to find b²:
Take the expression
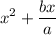
We can also write it as:
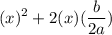
According to the formula
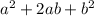 , the b of this expression is
, the b of this expression is
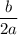 . So,
. So,
b² will be:
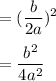
So, we will add
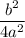 to both sides in Eq. (1)
to both sides in Eq. (1)
For STEP 4, the equation will become:
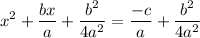
![\rule[225]{225}{2}](https://img.qammunity.org/2023/formulas/english/college/eq413d752mwtrwwenrzwldxt4w1olmf1b3.png)