Question

4/10x - 2x + 8/5 = 4/5

Answer 1

`\large\displaystyle\text{$\begin{gathered}\sf \left((4)/(10)* x\right)-(2 * x)+(8)/(5)=(4)/(5) \end{gathered}$}`

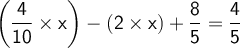
Reduce the fraction 4/10, to its minimum expression, extracting and canceling 2.

• 
  `\large\displaystyle\text{$\begin{gathered}\sf (2)/(5)x-2x+(8)/(5)=(4)/(5) \end{gathered}$}`

Combine
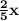`\bf{(2)/(5)x }` and -2x to get
`\bf{-(8)/(5)x}`.

• 
  `\large\displaystyle\text{$\begin{gathered}\sf -(8)/(5)x+(8)/(5)=(4)/(5) \ \end{gathered}$}`

Subtract 8/5 from both sides.

• 
  `\large\displaystyle\text{$\begin{gathered}\sf -(8)/(5)x=(4)/(5)-(8)/(5) \ \ \end{gathered}$}`

Since 4/5 and 5/8 have the same denominator, join their numerators to subtract them.

• 
  `\large\displaystyle\text{$\begin{gathered}\sf -(8)/(5)x=(4-8)/(5) \end{gathered}$}`

Subtract 8 from 4 to get -4.

• 
  `\large\displaystyle\text{$\begin{gathered}\sf -(8)/(5)x=-(4)/(5) \end{gathered}$}`

Multiply both sides by
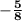`\bf{-(5)/(8)}`, the reciprocal of
`\bf{-(5)/(8)}`.

• 
  `\large\displaystyle\text{$\begin{gathered}\sf x=-(4)/(5)\left(-(5)/(8)\right) \end{gathered}$}`

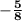Multiply -4/5 by -5/8 (to do this, multiply the numerator by the numerator and the denominator by the denominator).

• 
  `\large\displaystyle\text{$\begin{gathered}\sf x=(-4(-5))/(5*8) \ \to \ \ Multiply \end{gathered}$}`
• 
  `\large\displaystyle\text{$\begin{gathered}\sf x=(20)/(40) \end{gathered}$}`

Reduce the fraction 20/40 to its lowest expression by extracting and canceling 20.

• 
  `\boxed{\large\displaystyle\text{$\begin{gathered}\sf x=(1)/(2) \end{gathered}$}}`

• Good luck in your studies