Answer:
Original fraction = ⁴/₇
Explanation:
Numerator: top of the fraction
Denominator: bottom of a fraction
Let x be the original numerator.
If the denominator of a fraction exceeds the numerator by 3:
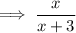
If the numerator is doubled and the denominator is increased by 14, then fraction becomes 2/3rd of the original fraction:
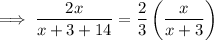
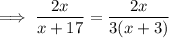
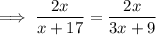
Cross multiply:
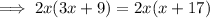
Divide both sides by 2x:

Subtract x from both sides:
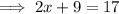
Subtract 9 from both sides:
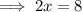
Divide both sides by 2:
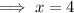
Substitute the found value of x into the original fraction:
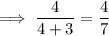
Therefore, the original fraction is ⁴/₇.