Question

. A bargain hunter purchases a "gold" crown at a flea market. After she gets home, she hangs it from a scale and finds its weight to be 7.84 N. She then weighs the crown while it is immersed in water, as shown below in Figure, and now the scale reads 6.86 N. Is the crown made of pure gold? Find the density of the crown and compare it to the density of gold. wag PODECID LE B water​

Answer 1

Average density of the crown: approximately
`8\; {\rm g \cdot mL^(-1)}`.

Hence, if this crown contains no empty space, this crown is not made of pure gold.

Step-by-step explanation:

Let
`m(\text{crown})` and
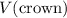`V(\text{crown})` denote the mass and volume of this crown. Let
`g` denote the gravitational field strength.

Since this crown is fully immersed in water, the volume of water displaced
`V(\text{water, displaced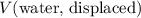})` is equal to the volume of this crown:

`V(\text{water, displaced}) = V(\text{crown})`.

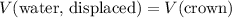The mass of water displaced would be:

`\begin{aligned}m(\text{water, displaced}) &= \rho(\text{water}) \, V(\text{water, displaced}) \\ &= \rho(\text{water}) \, V(\text{crown})\end{aligned}`.

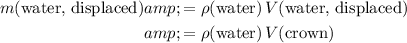The weight of water displaced would be
`m(\text{water, displaced})\, g = \rho(\text{water}) \, V(\text{crown})\, g\end{aligned}`.

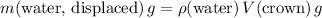The buoyancy force on this crown is equal to the weight of water that this crown displaced:

`F(\text{buoyancy}) = \rho(\text{water}) \, V(\text{crown})\, g`.

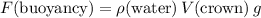The magnitude of this buoyancy force is
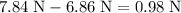`7.84\; {\rm N} - 6.86\; {\rm N} = 0.98\; {\rm N}`. Rearrange the equation for buoyancy to find
`V(\text{crown})`:

`\begin{aligned} V(\text{crown}) &= \frac{F(\text{buoyancy}) }{\rho(\text{water}) \, g}\end{aligned}`.

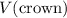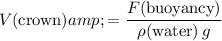Since the weight of this crown is
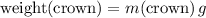`\text{weight}(\text{crown}) = m(\text{crown})\, g`, the mass of this crown would be
`m(\text{crown})= \text{weight}(\text{crown}) / g`.

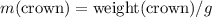The average density of this crown would be:

`\begin{aligned}\rho(\text{crown}) &= \frac{m(\text{crown})}{V(\text{crown})} \\ &= \frac{\text{weight}(\text{crown}) / g}{F(\text{buoyancy}) / (\rho(\text{water})\, g)} \\ &= \frac{\text{weight}(\text{crown})}{F(\text{buoyancy})}\, \rho(\text{water}) \\ &= \frac{7.84\; {\rm N}}{0.98\; {\rm N}}* 1.000 \; {\rm g\cdot mL^(-1)} \\ &= 8.0\; {\rm g \cdot mL^(-1)}\end{aligned}`.

The density of pure gold is significantly higher than
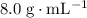`8.0\; {\rm g\cdot mL^(-1)}`. Hence, if this crown contains no empty space (i.e., no air bubble within the crown), the crown would not be made of pure gold.