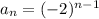Answer:
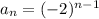
Explanation:
So a geometric sequence can be explicitly defined as:
 . IN this case we're given r, but we don't know what a_1 is. We can find this by lugging in 4 as n, and -8 as a_n, since they're given values
. IN this case we're given r, but we don't know what a_1 is. We can find this by lugging in 4 as n, and -8 as a_n, since they're given values
Plug known values in:
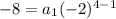
Subtract the values in the exponent
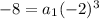
Simplify the exponent
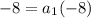
Divide both sides by -8
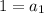
So the nth term can be defined as:
 , and since the 1 is redundant, the equation can simply be defined as:
, and since the 1 is redundant, the equation can simply be defined as: