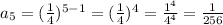Question

Find the indicated term of the geometric sequence.
5th term of 1,
1 /4,1/16,…

Answer 1

`(1)/(256)`

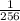
Explanation:

So generally a geometric sequence can be defined as:
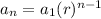`a_n=a_1(r)^(n-1)` which is the explicit form. The r, is what each previous term is being multiplied by to get the next value which is evident in the recursive form:
`a_n = r(a_(n-1))\\`. Knowing this we can take two values which are "next" to each other to find what r is. In this case I'll just is 1 and 1/4, given these two values we know that:
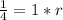`(1)/(4) = 1 * r`, 1*r is just r... so what each term is being multiplied by is 1/4. So let's plug the values into the explicit formula:
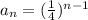`a_n=((1)/(4))^(n-1)` (I didn't put an a_1 value in front, since it's just 1... so it's a bit redundant). Anyways using this formula we simply plug in 5 as n into the equation to find the 5th term:
`a_5 = ((1)/(4))^(5-1) = ((1)/(4))^4 = (1^4)/(4^4) = (1)/(256)`