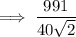Answer:
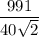
Explanation:
Given expression:
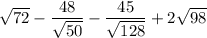
Rewrite 72 as 36·2, 50 as 25·2, 128 as 64·2 and 98 as 49·2:
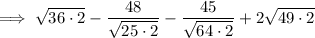
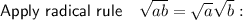
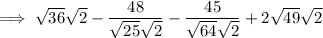
Rewrite 36 as 6², 25 as 5², 64 as 8² and 49 as 7²:
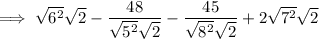
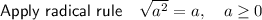
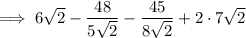
Simplify:
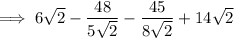
Combine like terms:
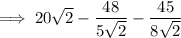
Make the denominators of the two fractions the same:
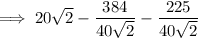
Rewrite 20√2 as a fraction with denominator 40√2:
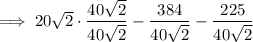
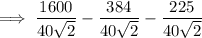
Combine fractions: