1. Find the domain and range of the function f(x)=√1-4x². - QAmmunity.org

1. Find the domain and range of the function f(x)=√1-4x².

asked Sep 8, 2023 65.9k views

2 Answers

Answer:

$\textsf{Domain}: \quad \left[-(1)/(2), (1)/(2)\right]$

$\textsf{Range}: \quad [0, 1]$

Explanation:

Domain: set of all possible input values (x-values)

Range: set of all possible output values (y-values)

Given function:

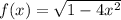
f(x)=√(1-4x^2)

As negative numbers don't have real square roots:

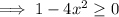
$\implies 1-4x^2\geq 0$

Therefore, to find the domain, solve the inequality.

Subtract 1 from both sides:

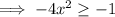
$\implies -4x^2\geq -1$

Divide both sides by -1 (reverse the inequality):

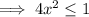
$\implies 4x^2 \leq 1$

Divide both sides by 4:

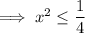
$\implies x^2\leq (1)/(4)$

$\textsf{For }\:a^n \leq b,\:\:\textsf{if }n\textsf{ is even then }-\sqrt[n]{b} \leq a \leq \sqrt[n]{b}:$

$\implies -\sqrt[2]{(1)/(4)} \leq x \leq \sqrt[2]{(1)/(4)}$

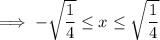
$\implies -\sqrt{(1)/(4)} \leq x \leq \sqrt{(1)/(4)}$

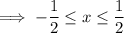
$\implies -(1)/(2) \leq x \leq (1)/(2)$

Therefore:

$\textsf{Domain}: \quad \left[-(1)/(2), (1)/(2)\right]$

To find the range, input the endpoints of the domain into the function:

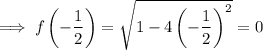
$\implies f\left(-(1)/(2)\right)=\sqrt{1-4\left(-(1)/(2)\right)^2}=0$

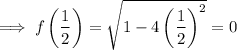
$\implies f\left((1)/(2)\right)=\sqrt{1-4\left((1)/(2)\right)^2}=0$

To find the limit of the range, find the extreme point(s) of the function by differentiating the function and setting it to zero.

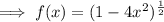
$\implies f(x)=(1-4x^2)^{(1)/(2)}$

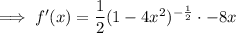
$\implies f'(x)=(1)/(2)(1-4x^2)^{-(1)/(2)} \cdot -8x$

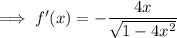
$\implies f'(x)=-(4x)/(√(1-4x^2))$

Setting it to zero and solving for x:

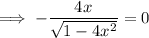
$\implies -(4x)/(√(1-4x^2))=0$

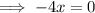
$\implies -4x=0$

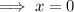
$\implies x=0$

Substitute x = 0 into the function:

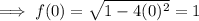
$\implies f(0)=√(1-4(0)^2)=1$

Therefore, the range is [0, 1]

1. Find the domain and range of the function f(x)=√1-4x².-example-1

Will Brode answered Sep 12, 2023

6.3k points

Search QAmmunity.org