Question

PLEASE HELP 70 points

Please show your work and take a screenshot or picture of the answer. Don't just type it in.

Answer 1

`\displaystyle \sum_(n=1)^(15) (2n-1) = 2 \sum_(n=1)^(15) n - \sum_(n=1)^(15)1`

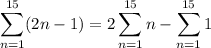
Recall that

`\displaystyle\sum_(n=1)^N 1 = N`

`\displaystyle \sum_(n=1)^N n = \frac{N(N+1)}2`

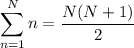
Then

`\displaystyle \sum_(n=1)^(15) (2n-1) = 2\cdot\frac{15\cdot16}2 - 15 = \boxed{225}`

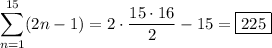
Alternatively, notice that the terms in the sum are odd integers, and terms on opposite ends of the sum add up to 30, except the middle term:

1 + 3 + 5 + 7 + … + 23 + 25 + 27 + 29

= (1 + 29) + (3 + 27) + (5 + 25) + … + (13 + 17) + 15

= [30 + 30 + 30 + … + 30] + 15

= 7×30 + 15

= 210 + 15

= 225