Question

Are the triangles similar? If so, state the similarity and the postulate or theorem that justifies your answer.

Answer 1

Answer: The triangles are not similar.

Explanation:

Two figures are similar simply if they have the same shape, but not necessarily the same size. In a more mathematical sense, similar figures have the same angle measures and proportionate side lengths.

For reference, side lengths are proportionate when the ratios between corresponding/matching sides are the same.

Since we do not have any angles, we will try using the SSS Similarity Theorem, which states that if all three sides of both triangles are in proportion, then the triangles are similar. We will first list all the side lengths and match corresponding ones.

`\triangle ABC \rightarrow 18,20,32\\ \triangle UVT \rightarrow 14,15,24`

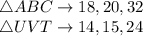
Since we matched corresponding sides, we can now check whether they have the same ratio).

`(18)/(14)=(20)/(15)=(32)/(24)`

`(9)/(7)=(4)/(3)=(4)/(3)`

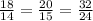
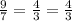
Not all of the side lengths have the same ratio, so these triangles aren't similar. you must multiply 14 by 9/7 to get to 18, but you need to multiply the other two sides by 4/3 to get to their