Question

Solve for w, where w is a real number.

Answer 1

Answer: w=9.

Explanation:

`√(-4w+61)=w-4`

Tolerance range:

`\left \{ {{-4w+61\geq 0} \atop {w-4\geq 0}} \right. \ \ \ \ \left \{ {4w\leq 61\ \atop {w\geq 4}} \right. \ \ \ \ \left \{ {{w\leq 15,25} \atop {w\geq 4}} \right. \ \ \ \ \Rightarrow\ \ \ \ \\w\in[4;15,25].`

Solution:

`(√(-4w+61))^2=(w-4)^2\\-4w+61=w^2-2*w*4+4^2\\-4w+61=w^2-8w+16\\w^2-4w-45=0\\D=(-4)^2-4*1*(-45)\\D=16+4*45\\D=16+180\\D=196.\\√(D)=√(196)\\√(D)=14 \\w_(1,2)=(-(-4)б14)/(2) \\w_1=(4-14)/(2) \\w_1=(-10)/(2) \\w_1=-5\ \\otin tolerance\ range.\\w_2=(4+14)/(2)\\ w_2=(18)/(2) \\w_2=9\ \in tolerance \ range.`

Answer 2

w= 9

Explanation:

`√( - 4w + 61) = w - 4`

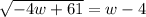
Square both sides:

-4w +61= (w -4)²

`\boxed{(a - b)^(2) = a^2 -2ab + b^2 }`

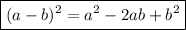
Expand:

-4w +61= w² -2(w)(4) +4²

-4w +61= w² -8w +16

Simplify:

w² -8w +16 +4w -61= 0

w² -4w -45= 0

Factorize:

(w -9)(w +5)= 0

w -9= 0 or w +5= 0

w= 9 or w= -5 (reject)

Note:

-5 is rejected since we are only taking the positive value of the square root here. If the negative square root is taken into consideration, then w= -5 would give us -9 on both sides of the equation.

Why do we use negative square root?

When solving an equation such as x²= 4,

we have to consider than squaring any number removes the negative sign i.e., the result of a squared number is always positive.

In the case of x²= 4, x can be 2 or -2. Thus, whenever we introduce a square root, a '±' must be used.

However, back to our question, we did not introduce the square root so we should not consider the negative square root value.