Question

Ignore 3/4 can someone please explain

Answer 1

Answer: 1/6

Step-by-step explanation:

The question is asking how much of the whole circumference is arc AB given that it's central angle is 60°. We can see that the angle is
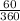`(60)/(360)` of the whole. This means that if there were 360 equal sectors, or slices, of the circle, then this angle would take 60 of them.

From this, we can see that if the circumference was divided into 360 equal parts, then the arc would also take up 60 of them, making the arc
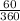`(60)/(360)`, or
`(1)/(6)`.

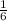We could have alternatively seen that the ratio of arc length to the whole circumference would be the same as the ratio of the central angle to the "whole angle" or 360°.

`\frac{Arc\hspace{0.1cm}Length}{Circumference}=\frac{Central\hspace{0.1cm}Angle}{360}`

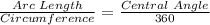
Putting in 60 for the central angle, we get

`\frac{Arc\hspace{0.1cm}Length}{Circumference}=(6)/(360)=(1)/(6)`

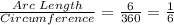
The question is asking what fraction of the circumference is the arc length, so let's isolate the arc length by multiplying the circumference to both sides

`Arc\hspace{0.1cm}Length=(1)/(6)*Circumference`

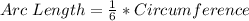
This equation in words says that the arc length is one sixth of the circumference, which is exactly what the question is asking.