Answer:
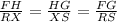
Explanation:
The order of the letters matters in any similarity theorem.
When triangle FHG is similar to triangle RXS, the lengths of FH must be similar to RX.
When 2 similar lines are divided, that number is the factor by which one triangle can be dilated to match the other.
That being said, each of these proportion statements can be read as individual division expressions that equal the next division expression.
This means
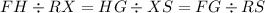 .
.
If you look at it this way, you can see that the sides you need to fill in must be the corresponding similar sides, so that you end up with the factor for the dilation of the 2 triangles.