Question

This figure represents a design found in a glass panel. ABCD is a rectangle with

midpoints X, Y, Z, and W. Emily states that the quadrilateral formed by the segments
that join the midpoints of the sides is a rhombus. Do you agree with her? Explain why
or why not.

Answer 1

Answer: Yes

Explanation:

Since ABCD is a rectangle,
`\angle AXY`,
`\angle YBZ`,
`\angle WCZ`, and
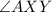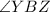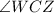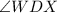`\angle WDX` are all right angles, and are thus all congruent because all right angles are congruent. Furthermore, because ABCD is a rectangle, we know that
`\overline{AB} \cong \overline{CD}` and
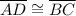`\overline{AD} \cong \overline{BC}`. Because we are given that X, Y, Z, and W are midpoints, using the fact that halves of congruent segments are congruent, we can conclude that
`\overline{AY} \cong \overline{YB} \cong \overline{CW} \cong \overline{WD}` and that
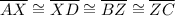`\overline{AX} \cong \overline{XD} \cong \overline{BZ} \cong \overline{ZC}`. As a result, we can conclude that
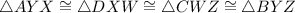`\triangle AYX \cong \triangle DXW \cong \triangle CWZ \cong \triangle BYZ` by SAS, and thus by CPCTC,
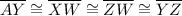`\overline{AY} \cong \overline{XW} \cong \overline{ZW} \cong \overline{YZ}`. Therefore, since the quadrilateral formed by the midpoints has four congruent sides, it must be a rhombus.