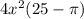Question

A family is having a pool built in their backyard. If their yard is rectangular and measures 10x by 10x and the pool is circular with a radius of 2x how much of the yard will be left over after the pool is built

Answer 1

`100x^2-4\pi x^2`

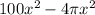
Also can be said as:

`4x^2(25-\pi )`

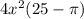
Explanation:

The scenario:

The question is asking you, "how much is left over."

In this scenario, you're going to have to subtract the area of the pool (P) from the total area of the backyard (B), which will leave you with the remaining area of the backyard (x).

This means your equation to solve this question is:

`x=B-P`

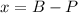
Step 1:

The value of B is the area of the backyard.

We are told that the backyard is a rectangular shape. So, we can use the formula of finding the area of a rectangle.

The formula is
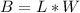`B=L*W`, where L is the length and W is the width.

Both the length and width are 10x, so we must plug that into this equation.

We end up getting:

`B=10x*10x`

Which can be simplified to:

`B=100x^2`

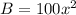
Step 2:

The value of P is the area of the pool.

The pool is a circular shape. So, to get the area of it, we must use the formula of finding the area of a circle.

The formula is
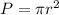`P=\pi r^2`, where r is the radius.

Plugging in the radius of 2x, we get:

`P=\pi (2x)^2`

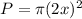
By solving this out, we end up with:

`P=4\pi x^2`

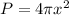
Step 3:

From the scenario, we have the equation:

`x=B-P`

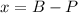
And from steps 1 and 2, we have the values:

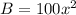`B=100x^2` and
`P=4\pi x^2`

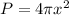
Now we just plug those values in to get:

`x=100x^2-4\pi x^2`

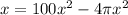
And finally, the amount of the backyard remaining is:

`100x^2-4\pi x^2`

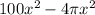
Different format:

This answer may be simplified to:

`4x^2(25-\pi )`