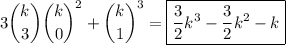Reduce the numbers in the list modulo 3 to get the set
{1, 2, 0, 1, 2, 0, …, 1, 2, 0}
containing
 copies each of 1, 2, and 0.
copies each of 1, 2, and 0.
Take any 3 elements from the list. Their sum is divisible by 3 if those elements' residues also sum to 3 ≡ 0 (mod 3). To get a sum of 0, we must make one of the following choices:
- 3 elements each with the same residue, so
0 + 0 + 0 ≡ 0 (mod 3)
1 + 1 + 1 ≡ 3 ≡ 0 (mod 3)
2 + 2 + 2 ≡ 6 ≡ 0 (mod 3)
- 1 element each with different residues, so
0 + 1 + 2 ≡ 3 ≡ 0 (mod 3)
There are
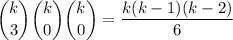
ways of choosing 3 elements with a given residue and 0 elements with any other residue, hence
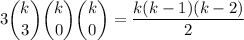
ways of choosing any 3 elements with the same residue, and there are
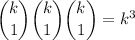
ways of choosing any 3 elements with distinct residues.
So, the total number of ways of making the selection is