Answer:
centre = (2, 9 ) , radius = 6
Explanation:
the equation of a circle in standard form is
(x - h)² + (y - k)² = r²
where (h, k ) are the coordinates of the centre and r is the radius
(x - 2)² + (y = 9)² = 36 ← is in standard form
with centre (2, 9 ) and r² = 36 ⇒ r =
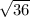 = 6
= 6