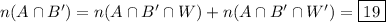1. Consult the linked question.
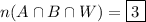 .
.
2. We have
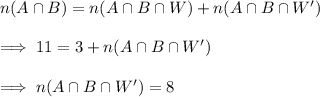
Similarly we can find
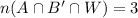
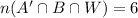
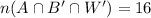
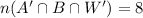
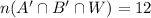
Then the total number of students that applied to at least two of the universities is
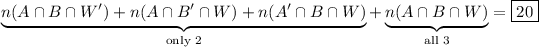
3. There's a small ambiguity here. Are we interested in students that applied to zero universities? If so, there are
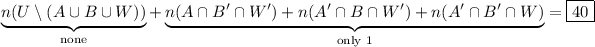
If we want students that applied to at least 1 school, we omit the first term and get a total of 36.
4. Split this set of students into those that also applied to Wachemo and those that did not.