Question

I really need help with this question

Answer 1

Answer: 39 years

Explanation:

The father says that adding both of the digits in his age will be 3 times greater than adding both digits one year later. Before we even start answering the problem, this tells us that the father's age has 2 digits in it.

Let's represent the 10's digit with x, and the 1's digit with y. If the father's age was 45, for example, x would be 4 and y would be 5.

Let's first make an equation to represent this situation:

The sum of the digits of the father's age would be represented by x + y, as x and y are the 10's digit and 1's digit respectively.

The father's age next year would be one greater than the current year, which makes y become y + 1. Then, the sum of the digits would be x + y + 1.

Now, we must make the first equation 3 times larger than the second and solve for the sum.

`x + y = 3(x+y+1)\\ x+y=3(x+y)+3\\ 1(x+y)-3(x+y)=3\\ -2(x+y)=3\\ x+y=(3)/(-2)=-(3)/(2)`

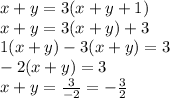
However, we can neither have a fraction or a negative as a sum of two digits in an age, as digits are always positive integers from 0 to 9.

This flaw came from the assumption that after 1 year, the sum of the digits will be x + y + 1. This isn't always true, as any number with its 1's digit of 9 turns into 0 the next year, and not 10. Instead, the x value increases by 1.

For example, someone the age 69 becomes 70 the next year, x increases by 1 and y becomes 0.

Let's make a new equation to try and see this.

We know that his current age has to have y = 9 for his new age to be y = 0. Therefore, the current sum of digits is x + 9.

The next year, we know that the 10's place will increase by 1 and the 1's place becomes 0. Therefore the sum of digits is x + 1 + 0, or x + 1.

Since the current sum of digits is 3 times greater than the sum next year, let's multiply the second equation by 3 to get equality. We just need to calculate the 10's digit, as the 1's digit is already 9.

`x+9 = 3(x+1)\\ x+9=3x+3\\ 9=2x+3\\ 6=2x\\ x=3`

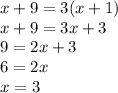
Since the 10's digit (or x) is 3 and the 1's digit (or y) is 9, the father's age is 39, and he will turn 40 next year.

Answer 2

39

Explanation:

I assume the father's age is a 2-digit number. He is not 9 years old or younger, and he is not 100 years old or older.

The sum of the digits of a two-digit number goes up by 1 from one number to the next unless the number ends in 9.

For example, from 17 to 18, the sum of the digits goes from 8 to 9.

If the number ends in 9, for example, 29, the digits add to 11. Then the next number is 30, and now the sum of the digits is 3, which is less than 11.

The father's age now is a number whose sum of digits is not only greater than the sum of the digits next year, but it is 3 times greater.

Let's look at 2-digit number and the next number and the sum of their digits.

19, 20; sums: 10, 2; 10/2 = 5, not 3

29, 30; sums: 11, 3; 11/3 ≠ 3

39, 40; sums: 12, 4; 12/4 = 3

Answer: The father is 39 years old.