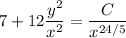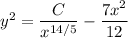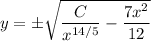I'm guessing the equation should read something like
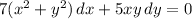
or possibly with minus signs in place of +.
Multiply both sides by
 to get
to get
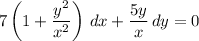
Now substitute
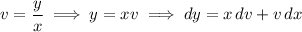
to transform the equation to
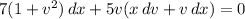
which simplifies to
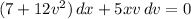
The ODE is now separable.
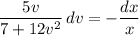
Integrate both sides. On the left, substitute

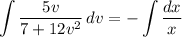

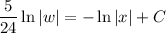
Solve for
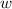 .
.

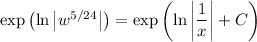
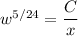
Put this back in terms of
 .
.
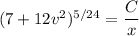
Put this back in terms of
 .
.

Solve for
 .
.