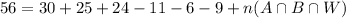Let A, B, and W denote the sets of students apply to Addis Ababa Uni (A), Bahir Dar Uni (B), or Wachemo Uni (W). Let U denote the universal set of all students in the class.
We're given the cardinalities of several sets:
• total number of students:
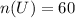
• A applicants:
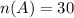
• B applicants:
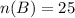
• W applicants:

• A and B applicants:

• A and W applicants:
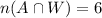
• B and W applicants:
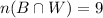
• non-applicants:
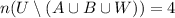
The last cardinality tells us
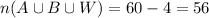 students applied anywhere at all.
students applied anywhere at all.
We want to find
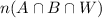 , the number of students that applied to each of the three universities.
, the number of students that applied to each of the three universities.
By the inclusion/exclusion principle,
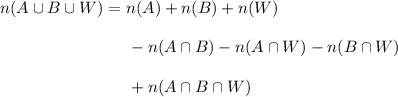
That is, we count up all the students in the sets A, B, and W, then subtract the number of students in each pairwise intersection to not double-count, then add back the number of students in the intersection of all three sets since it was removed in the previous step.
Now solve.