It's kind of self-evident. Any power of 21 will have a 1 in the units place, and adding 9 to it makes it 0 and hence the number is divisible by 5.
To prove the claim by induction, first establish the base case. I assume
 , so for
, so for
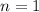 we have
we have

and of course 30 = 5×6 is divisible by 5.
Assume the claim is true for
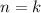 , that
, that
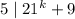 . This means that for some integer
. This means that for some integer
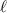 , we can write
, we can write
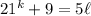
Now the induction step: when
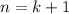 , we have
, we have
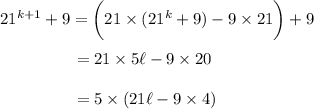
which is divisible by 5. QED