Question

Y is inversely proportional to x².
When x = 4, y = 2.
Find y when x = 1 divided by 2

Answer 1

`\textbf{Heya !}`

✏
`\bigstar\textsf{Given:-}`✏

• y is inversely proportional to
  `\sf{x^2}`.

✏
`\bigstar\textsf{To\quad find:-}` ✏

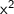• If y=2 when x=4, what is y when x=
  `(1)/(2)` ?

▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪

✏
`\bigstar\textsf{Solution\quad steps:-}` ✏

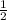If y is inversely proportional to x^2, the equation looks as shown below:-

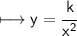`\sf{\longmapsto{y=\cfrac{k}{x^2}}`, where k -- constant of proportionality

Plug in all values

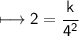`\sf{\longmapsto{2=\cfrac{k}{4^2}}` , simplifying --

`\sf{\longmapsto{2=k/16}`

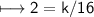
multiply by 16 both sides

`\sf{\longmapsto 2*16=k}}`

`\sf{\longmapsto{32=k}}`

▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪

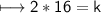
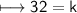
Plug 32 into the second equation:-

`\sf{\longmapsto y=\cfrac{32}{\bigg(\cfrac{1}{2}\bigg)^2}}`

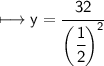
simplify the complex fraction

`\longmapsto\sf{y=\cfrac{32}{\cfrac{1}{4}}`

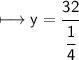
divide fractions

`\sf{\longmapsto{y=\cfrac{32}{1}/\cfrac{1}{4}}=\cfrac{32}{1}\cdot}\cfrac{4}{1}}=128}`

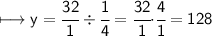
`hope that was helpful to u ~