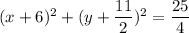Circle Equations
Generally, the equation of a circle is organized like this:
 , where (h,k) is the centre and r is the radius.
, where (h,k) is the centre and r is the radius.
Solving the Question
We're given the endpoints of the diameter:
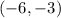 and
and
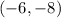 .
.
First, we can find the centre of the circle by finding the midpoint of these two endpoints.
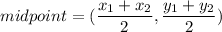
Plug in the points:
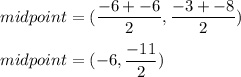
Therefore, the centre of the circle is
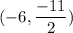 . Plug this into the general equation:
. Plug this into the general equation:
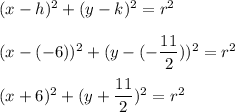
To find the radius of the circle, we can calculate the distance between the centre and one of the given endpoints:

Plug in the centre and one of the endpoints:
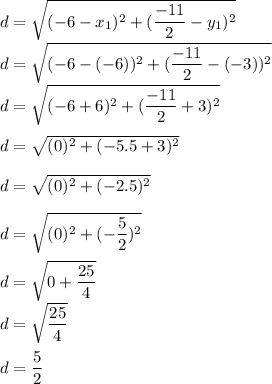
Therefore, the radius of the circle is
 . Plug this into the general equation:
. Plug this into the general equation:
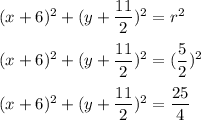
Answer