Question

The difference of the square of a number and 8 is equal to 8 times that number. Find the positive solution.

Answer 1

83758263983639483883

Answer 2

`2√(6) +4`

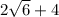
Explanation:

Let x be that unknown number.

From the information given from the question, we can deduce:

`x^(2) -8=8x`

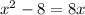
From here, we can solve for x to find what is the number.

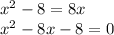`x^(2) -8=8x\\x^(2) -8x-8=0` (Quadratic Equation)

From here we can use the Quadratic Formula to solve for x.

`x=\frac{-b+/-\sqrt{b^(2) -4ac} }{2a}`

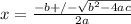
In this case,

a = 1, b = -8 , c = -8

We substitute a, b and c to find x.

`x=\frac{-(-8)+/-\sqrt{(-8)^(2)-4(1)(-8) } }{2(1)} \\= 2√(6) +4`

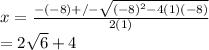
(Reject the negative solution)