Find the area of the region defined by the region defined by the inequality 2|x| + 3|y-1| ≤ 6

Question

asked Jun 25, 2023 111k views

1 Answer

RichardHowells · Answer 1 · 2023-07-02T02:54:06+0000

If
and
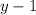y-1 have the same sign, then either

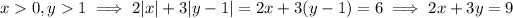
$x>0,y>1 \implies 2|x| + 3|y-1| = 2x + 3(y-1)=6 \implies 2x + 3y = 9$

or

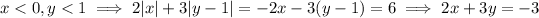
$x<0,y<1 \implies 2|x| + 3|y-1| = -2x - 3(y-1) = 6 \implies 2x + 3y = -3$

If
and
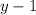y-1 have opposite sign, then

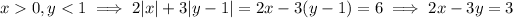
$x>0,y<1 \implies 2|x| + 3|y-1| = 2x - 3(y-1) = 6 \implies 2x -3y = 3$

or

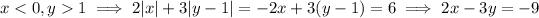
$x<0,y>1 \implies 2|x| + 3|y-1| = -2x + 3(y-1) = 6 \implies 2x-3y = -9$

This is to say that the region has boundaries given by these two sets of parallel lines, so we can equivalently describe the region with the set

$R = \left\{(x,y) \mid -3\le2x+3y\le9 \text{ and } -9\le2x-3y\le3\right\}$

The area of
is given by the double integral

$\displaystyle \iint_R dx\,dy$

To compute the area, change the variables to

$\begin{cases}u = 2x + 3y \\ v = 2x - 3y\end{cases} \implies \begin{cases}x = \frac14(u+v) \\ y = \frac16(u-v)\end{cases}$

The Jacobian for this transformation is

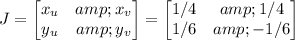
$J = \begin{bmatrix} x_u & x_v \\ y_u & y_v \end{bmatrix} = \begin{bmatrix}1/4 & 1/4 \\ 1/6 & -1/6\end{bmatrix}$

with determinant
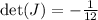$\det(J) = -\frac1{12}$ . Then the integral transforms to

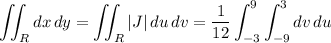
$\displaystyle \iint_R dx\,dy = \iint_R |J| \, du \, dv = \frac1{12} \int_(-3)^9 \int_(-9)^3 dv\, du$

which is 1/12 the area of a square with side length 12. Hence the integral evaluates to

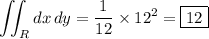$\displaystyle \iint_R dx\,dy = \frac1{12}*12^2 = \boxed{12}$ .