Question

Select the equivalent expression. (Please Help!!!)

(a/b^3)^4 = ?
Choose 1 answer:
A. a^8/b^8
B. a^4/b^12
C. a/b^81
D. a^5/b^7

Answer 1

`\large\displaystyle\text{$\begin{gathered}\sf \left((a)/(b^(3) )\right)^(4) \end{gathered}$}`

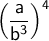
Use the rules of exponents to simplify the expression.

• 
  `\large\displaystyle\text{$\begin{gathered}\sf \left((a^(1) )/(b^(3))\right)^(4) \end{gathered}$}`

To raise the quotient of two numbers to a power, raise each power to the power and then divide it.

• 
  `\large\displaystyle\text{$\begin{gathered}\sf ((a^(1))^(4) )/((b^(3))^(4) ) \end{gathered}$}`

To raise a power to another power, multiply the exponents.

• 
  `\large\displaystyle\text{$\begin{gathered}\sf (a^(4) )/(b^(3*4) ) \end{gathered}$}`

Multiply 3 by 4.

• 
  `\boxed{\large\displaystyle\text{$\begin{gathered}\sf (a^(4) )/(b^(12) ) \end{gathered}$}}`

We conclude that: the correct option is "B".

Answer 2

Answer: B. a^4/b^12

Explanation: