Answer:
The magnitude of the magnetic field at the point P is
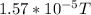 and the field is pointing into the page.
and the field is pointing into the page.
Step-by-step explanation:
The general form of a similar question to this is:
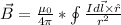
where
 is the vector of the Magnetic Field,
is the vector of the Magnetic Field,
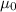 is the Free Space Permeability Constant (equal to
is the Free Space Permeability Constant (equal to
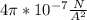 ),
),
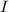 is the current, and
is the current, and
 is the distance from the segment to the point P. (I will get to the
is the distance from the segment to the point P. (I will get to the
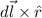 term in a bit)
term in a bit)
This equation is fairly complicated. Luckily, it can be simplified by looking at the magnitude and direction separately.
The first thing to simplify is the cross product. Due to the fact that a cross product can be simplified from
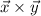 to
to
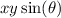 , where
, where
 is the angle between the 2 vectors, and
is the angle between the 2 vectors, and
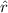 is the unit vector of
is the unit vector of
 (i.e.
(i.e.
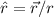 ) we can simplify
) we can simplify
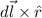 to just
to just
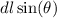 .
.
Next, we will look at the integral. In this scenario, everything will function as a constant, so we can essentially ignore it.
Finally,
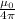 simplifies down to
simplifies down to
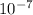 .
.
This gives us our new equation for the Magnetic Field produced by a single segment at a point:

Now we need to find values for
 and
and
 . Luckily, we are dealing with a 45-45-90 triangle with sides of
. Luckily, we are dealing with a 45-45-90 triangle with sides of
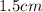 . This means the distance
. This means the distance
 is
is
 ! Similarly, because it is a 45-45-90 triangle, our
! Similarly, because it is a 45-45-90 triangle, our
 is
is
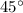 !
!
Now we can start plugging things in:
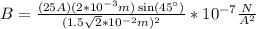
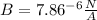 or
or
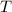
This is the magnitude due to only one single segment. In order to find the total field, we need to know the direction of the field due to each segment.
Finding the direction is really easy. Just use the right hand rule. Point your thumb in the direction of the current and curl the rest of your fingers around an imaginary pole. The direction your fingers point is the direction of the field. In this case, the field lines due to the segments point into the page in the 4th quadrant (the origin is the bend). This means that at point P, both segments induce the same field in the same direction. Therefore, we can take our value from before and double it, giving us our final answer:
 ; into the page.
; into the page.