Question

If 4 is the solution set of the equation x² -4 = 0 and B is

the solution set of the equation x²-3x+2=0, how many
elements are in the union of the two sets?
A. 1
C. 3
B. 2
D. 4

Answer 1

3 elements

Explanation:

Let A = solution set of x²-4

B = solution set of x²-3x+2

First, find the solution of each sets:

`\displaystyle{x^2-4=0}\\\\\displaystyle{(x+2)(x-2)=0}\\\\\displaystyle{x=2,-2}`

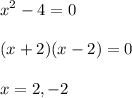
Set B:

`\displaystyle{x^2-3x+2=0}\\\\\displaystyle{(x-2)(x-1)=0}\\\\\displaystyle{x=1,2}`

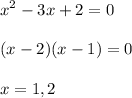
Now we can write new set as:

A = {2, -2}

B = {1, 2}

The union of A and B means combine both sets together:

A ∪ B = {2, -2, 1, 2}

However, in a set, we do not write duplicate elements, so the union set will be:

A ∪ B = {2, -2, 1}

Hence, there are 3 elements in A ∪ B.