Answer:
max{x²-4x²+5} = 5 at x = 0
Explanation:
1. Find the critical numbers by finding the first derivative of f(x), set it to 0 and solve for x.

We get:
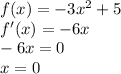
So the critical number is x = 0.
2. Evaluate the first derivative by plugging in the critical number and see if the derivative is positive or negative on both sides:
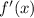 is positive when the x < 0 (for example: -6*(-1)=+)
is positive when the x < 0 (for example: -6*(-1)=+)
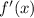 is negative when the x > 0 (for example: -6*(1)=-)
is negative when the x > 0 (for example: -6*(1)=-)
Therefore, you have a local maximum.
Now just get the Y value by plugging in the critical number in the original function.
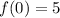
local maximum is (0,5)