Question

Answer these two questions pls

Thank you if your able to answer! :)

Q1) Find the LCM and HCF of the following by using prime factorisation method.
(i) 12,18
(ii) 12,15 and 21
Q2) If LCM (16, y) = 48 and HCF (16, y) = 12
Find y. ​

Answer 1

`{\large{\textsf{\textbf{\underline{\underline{Question \: 1 :}}}}}}`

`\diamond\:{\boxed{\tt{\purple{{ part \:(i) :}}}}}`

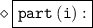
❍ Prime factorisation :-

‣ Prime factors of 12 -

‣ Prime factors of 18 -

Therefore,

`\star \: 12 = {2}^(2) * {3}^(1)`

`\star \: 18= {2}^(1) * {3}^(2)`

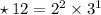
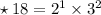
✧ LCM of 12 and 18 =
`\sf {2}^(2) * {3}^(2)`

`\implies 36`

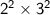
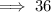
✧ HCF of 12 and 18 =
`\sf {2}^(1) * {3}^(1)`

`\implies 6`

`\diamond\:{\boxed{\tt{\red{{ part \:(ii) :}}}}}`

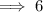
❍ Prime factorisation :-

‣ Prime factors of 12 -

‣ Prime factors of 15 -

‣ Prime factors of 21 -

Therefore,

`\star \: 12 = {2}^(2) * {3}^(1)`

`\star \: 15 = {3}^(1) * {5}^(1)`

`\star \: 21 = {3}^(1) * {7}^(1)`

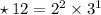
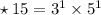
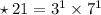
✧ LCM of 12, 15 and 21 =
`\sf {2}^(2) * {3}^(1) * {5}^(1) * {7}^(1)`

`\implies 420`

✧ HCF of 12, 15 and 21 =
`\sf {3}^(1)`

`\implies 3`

`{\large{\textsf{\textbf{\underline{\underline{Question \: 2 :}}}}}}`

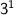
Using,

LCM × HCF = Product of two given numbers

Putting the values,

`\longrightarrow \sf 48 * 12 = 16 * y`

`\longrightarrow \sf \frac{ \cancel{48} _(3) * 12}{ \cancel{16}{ _1} } = y`

`\longrightarrow \sf y = 3 * 12`

`\longrightarrow {\sf{{{\boxed{\green{\bold {\sf y = 36 }}}}}}}`

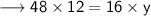
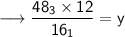
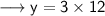
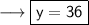
Therefore,

The value of y = 36

`{\large{\textsf{\textbf{\underline{\underline{Important \: points :}}}}}}`

• A natural number "P" > 1 having only two factor one and "P" itself is called prime number.

• A prime number is never negative.

• H.C.F is the product of smallest power of each common prime factor.

• L.C.M is the product of greatest power of each prime factor.

• HCF is always a factor of LCM.

`\underline{\rule{300pts}{3pt}}`