Explanation:
Let take the first derivative

The second derivative

The third derivative
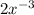
The fourth derivative
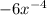
The fifth derivative
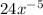
Let create a pattern,
The values always have x in it so
our nth derivative will have x in it.
The nth derivative matches the negative nth power so the nth derivative so far is
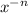
Next, lok at the constants. They follow a pattern of 1,2,6,24,120). This is a factorial pattern because
1!=1
2!=2
3!=6
4!=24
5!=120 and so on. Notice how the nth derivative has the constant of the factorial of the precessor
so our constant are

So far, our nth derivative is
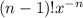
Finally, notice for the odd derivatives we are Positve and for the even ones, we are negative, this means we are raised -1^(n-1)
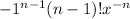
That is our nth derivative