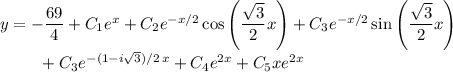The given differential equation has characteristic equation

Solve for the roots
 .
.
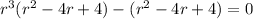

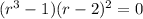
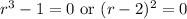
The first case has the three cubic roots of 1 as its roots,
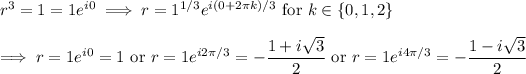
while the other case has a repeated root of
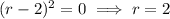
Hence the characteristic solution to the ODE is
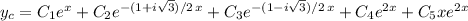
Using Euler's identity
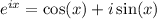
we can reduce the complex exponential terms to
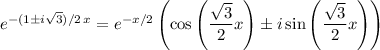
and thus simplify
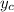 to
to

For the non-homogeneous ODE, consider the constant particular solution
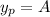
whose derivatives all vanish. Substituting this into the ODE gives

and so the general solution to the ODE is